Теоретически, как указывалось выше, для большинства периодических функций спектр неограничен, т.е. для передачи сигналов телемеханики без изменения формы необходимы бесконечно большая полоса пропускания канала связи и отсутствие амплитудных и фазовых искажений. Практически все каналы связи имеют ограниченную полосу пропускания, и форма сигналов при передаче по каналу изменяется даже при отсутствии в этой полосе амплитудных и фазовых искажений. Очевидно, важно передать ту часть спектра сигнала, которая содержит гармонические составляющие с относительно большими амплитудами. В связи с этим вводится понятие практической ширины спектра сигнала. Под практической шириной спектра сигнала понимается та область частот, в пределах которой лежат гармонические составляющие сигнала с амплитудами, превышающими наперед заданную величину.

Поскольку средняя мощность, выделяемая сигналом на активном сопротивлении, равном 1 Ом, складывается из мощностей, выделяемых на этом сопротивлении гармоническими составляющими,

практическая ширина спектра с энергетической точки зрения может быть определена как область частот, в пределах которой сосредоточена подавляющая часть мощности сигнала.

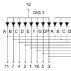
В качестве примера определим практическую ширину спектра периодической последовательности прямоугольных импульсов (рис. 1.8,а), если требуется учесть все гармонические составляющие сигнала, амплитуды которых более 0,2 от амплитуды первой гармоники. Число подлежащих учету гармоник k может быть получено из выражения

,

откуда k = 5.

Таким образом, практическая ширина спектра в рассмотренном примере оказывается равной 5W 1 , в ней размещаются всего три гармоники (первая, третья и пятая) и постоянная составляющая.

Средняя мощность P k 5 , выделяемая в активном сопротивлении, равном 1 Ом, перечисленными составляющими, равна

Средняя мощность, выделяемая в этом же сопротивлении всеми составляющими сигнала, будет

Таким образом, %, т.е. составляющие, входящие в практический спектр, выделяют в активном сопротивлении 96 % всей мощности сигнала.

Очевидно, расширение практического спектра данного сигнала (свыше 5W 1) с энергетической точки зрения нецелесообразно.

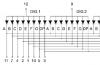
Ограничение спектра сигнала оказывает также влияние на его форму. Для иллюстрации на рис. 1.8 показано изменение формы прямоугольных импульсов при сохранении в спектре только постоянной составляющей и первой гармоники (рис. 1.8, б ), при ограничении спектра частотой 3W 1 (рис. 1.8, в ) и при ограничении спектра частотой 5W 1 (рис. 1.8, г ). Как следует из рисунка, чем круче должен быть фронт импульса, тем большее число высших гармонических составляющих должно входить в состав сигнала.

A 0 +A 1 (t )

A 0 +A 1 (t )+A 3 (t ) A 0 +A 1 (t )+A 3 (t)+A 5 (t )

		в		г

Рис. 1.8. Формы сигнала при ограничении спектра последовательности

прямоугольных импульсов

Рассмотренная зависимость формы периодического сигнала от количества суммируемых гармоник показывает, что при выборе практической ширины спектра сигнала нельзя ограничиваться только энергетическими соображениями. Необходимо учитывать требования к сигналу на выходе системы, как с энергетической точки зрения, так и с точки зрения сохранения его формы. В общем случае практическая ширина спектра сигнала выбирается из условия

, (1.21)

где m = 0,5… 2 – коэффициент формы импульса; при m = 1 обеспечивается передача около 90 % всей энергии сигнала.

В кодоимпульсных системах телеизмерения, а также во многих системах телеуправления каждая кодовая комбинация состоит из определенной последовательности прямоугольных импульсов и пауз. Кодовая комбинация, соответствующая данной величине измеряемого параметра или команде, может периодически передаваться по каналу связи. Спектр такого сигнала зависит, конечно, от того какая именно кодовая комбинация передается. Но самым главным фактором, определяющим удельный вес высших гармоник спектра, остается наибольшая частота следования импульсов. Поэтому и для кодоимпульсных систем при определении практически необходимой ширины полосы частот выбирают сигнал в виде периодической последовательности прямоугольных импульсов (рис. 1.5). Параметр t выбирают равным длительности самого короткого импульса среди всех встречающихся в кодовых комбинациях, период следования T = 2t. В этом случае наибольшая частота следования импульсов W max = 2p / T и частота основной гармоники спектра W 1 = W max . Необходимая ширина полосы частот сигнала определяется дискретным спектром с ограниченным числом составляющих и в соответствии с выражением (1.21).

Характер спектра, определяющий требуемую полосу частот, зависит не только от вида сигнала, но и от условий, существующих в тракте передачи. Если переходные процессы, возникающие в системе при передаче одного импульса, заканчиваются до момента возникновения следующего импульса, то вместо периодической последовательности импульсов можно рассматривать передачу независимых одиночных импульсов.

Спектр одиночного импульса имеет следующий вид:

Рис. 10.16. Спектр одиночного импульса

Из спектра одиночного импульса ясно, что чем меньше , тем шире спектр. При ® 0 – спектр равномерный; а при = – имеем на спектре одну постоянную составляющую.

Эта связь вытекает непосредственно из общего свойства преобразования Фурье.

Пусть ƒ(t ) соответствует спектр F (ω).

Изменим масштаб функции ƒ(t ) по оси времени в a раз и рассмотрим спектр функции a ƒ(at ):

заменим переменные at = z ; adt = dz ; t = z /a , то есть длительность функции ƒ(t ) уменьшится в a раз, во столько же раз возрастет ширина ее спектра.

Вопрос о соотношении между длительностью импульса и шириной его спектра имеет громадное практическое значение. В вычислительной технике необходимы короткие и мощные импульсы и в тоже время требуется, чтобы спектр импульса был как можно уже, так как широкие спектры вызывают трудности при создании аппаратуры.

Эти требования противоречивы.

Возникает вопрос: нельзя ли найти такие сигналы, которые обладали бы ограниченным спектром и одновременно ограниченной длительностью? Формализм преобразования Фурье этого не позволяет, однако для реальных сигналов могут быть введены разумные ограничения, которые позволяют ограничить либо Δt , либо Δƒ, либо и то и другое.

Наиболее удобным в этом смысле, как мы уже говорили ранее, является энергетический критерий. При этом можно представить себе следующие модели сигналов:

1. Сигналы ограничены во времени . Спектр – неограничен теоретически; физически он всегда ограничен и учитывается только та часть спектра, где сосредоточена подавляющая часть энергии сигнала.

2. Сигналы имеют ограниченный спектр , то есть математически это периодические, неограниченные во времени сигналы. Фактически, реальный процесс всегда ограничен во времени, поэтому учитывается только интервал времени, в котором сосредоточена подавляющая часть всей энергии сигнала.

где t 0 – часто задается естественно: для симметричного импульса t 0 = 0; для одиночного так же t 0 = 0 и формула имеет вид:

.

3. Сигналы, у которых и длительность (Δt ) и ширина спектра (Δƒ) ограничены как интервалы, в которых сосредоточена подавляющая часть энергии сигнала. Математический аппарат преобразования Фурье дает в этом случае приближенные разультаты.

При ограничениях по Δt и Δƒ можно поставить следующую задачу – отыскать такую форму сигнала, для которой произведение Δt · Δƒ достигает min.

Такому условию соответствует импульс, имеющий колоколообразную форму, которая описывается кривой Гаусса (кривой нормального распределения).

Рис. 10.17. Кривая Гаусса

Произведение Δt · Δƒ может быть уменьшено только до определенного предела:

Δt · Δƒ ≈ const > 0,

где const зависит от выбора определения Δƒ и Δt .

Приведем значения Δt · Δƒ для различных видов сигналов в предположении, что

,

где η = 0.9.

Δt · Δƒ – max для импульсов с разрывом (экспонента, прямоугольник); меньше для импульсов с разрывом в первой производной (треугольник и косинусоидальный) и наименьшее значение у колоколообразного импульса, у которого функция непрерывна со всеми своими производными. http://сайт/

Наиболее плодотворной и близкой к реальной действительности является модель с ограниченным спектром.

Этому способствует тот факт, что спектр мощности реального сигнала достаточно быстро спадает вне интервала частот, на который приходится основная часть мощности.

В инженерной практике принимают (в первом приближении независимо от формы сигнала):

Δt · Δƒ ≈ 1.

Практически, независимо от формы сигнала содержится > 90% энергии.

1. Если T имп = 3млсек, то какая требуется полоса частот, чтобы пропустить основную долю энергии?

.

2. Какова длительность телевизионных импульсов, если F TV max = 6мггц?

Из предыдущих параграфов уже ясно, что чем меньше длительность сигнала, тем шире его спектр. Для установления количественных соотношений между указанными параметрами сигнала необходимо условиться об определении понятий длительность сигнала и ширина его спектра. В практике применяются различные определения, выбор которых зависит от назначения сигнала, его формы, а также от структуры спектра. В некоторых случаях выбор является произвольным. Так, ширину спектра прямоугольного импульса определяют либо как основание главного лепестка (например, в п. 1 § 2.10), либо на уровне от максимального значения спектральной плотности. Длительность колоколообразного импульса (см. § 2.10, п. 3) и ширину его спектра иногда определяют на уровне 0,606 от максимального значения соответственно или . Часто пользуются энергетическим критерием, понимая под шириной спектра полосу частот, содержащую заданную долю полной энергии сигнала.

Для практики важное значение имеет также оценка протяженности «хвостов» спектра вне полосы частот, содержащей основную часть энергии сигнала.

1. ОПРЕДЕЛЕНИЕ ПРОИЗВЕДЕНИЯ ПОЛОСА Х ДЛИТЕЛЬНОСТЬ

Для выявления предельных соотношений, связывающих длительность сигнала и ширину спектра, в современной теории сигналов большое распространение получил метод моментов.

По аналогии с понятием момента инерции в механике эффективную длительность сигнала можно определить выражением

где середина импульса определяется из условия

Имеется в виду, что функция интегрируема с квадратом (сигнал с конечной энергией).

Аналогично эффективная ширина спектра определяется выражением

Так как модуль спектра не зависит от смещения во времени, можно положить Наконец, сигнал можно нормировать таким образом, чтобы его энергия Э равнялась единице и, следовательно,

При этих условиях выражения для и принимают вид

и, следовательно, произведение длительность x полоса

Нужно иметь в виду, что являются среднеквадратическими отклонениями соответственно от и . Поэтому полную длительность сигнала следует приравнять а полную ширину спектра (включая и область отрицательных частот) - величине .

Произведение зависит от формы сигнала, однако оно не может быть меньше 1/2. Оказывается, что наименьшее возможное значение соответствует колоколообразному импульсу.

Метод моментов применим не к любым сигналам. Из выражений для видно, что функция с увеличением t должна убывать быстрее, чем , а функция - быстрее, чем так как в противном случае соответствующие интегралы стремятся к бесконечности (расходятся).

В частности, это относится к спёктру строго прямоугольного импульса, когда

В этом случае выражение для не имеет смысла и оценку эффективной ширины спектра прямоугольного импульса приходится основывать на иных критериях.

Рассмотрим некоторые простые сигналы типа видеоимпульсов, т. е. сигналов, спектр которых сосредоточен в области низких частот, и определим с помощью равенства Парсеваля энергию, содержащуюся в полосе от до некоторой граничной частоты :

Относя затем к полной энергии импульса Э, определяем коэффициент

характеризующий концентрацию энергии в заданной полосе.

В качестве исходного сигнала примем прямоугольный импульс, затем рассмотрим треугольный и колоколообразный (гауссовский). Последний особенно показателен, так как для него обеспечивается максимально возможная концентрация энергии спектра в заданной полосе .

Для прямоугольного импульса в соответствии с (2.68)

Вычислив интеграл, получим

где - интегральный синус.

Переходя к аргументу , записываем

Для треугольного импульса, спектральная плотность которого определяется формулой (2.73), а полная энергия

Рис. 2.23. Доля энергии сигнала в полосе (а) и деформация импульса при усечении спектра (б)

Для гауссовского импульса в соответствии с (2.77) получаем

где - полная энергия гауссовского импульса, а функция

Учитывая, что длительность гауссовского импульса определена в п. 3 § 2.10 и равна , аргумент функции можно записать в форме Функции для трех импульсов представлены на рис. 2.23, а.

Итак, значение произведения требующееся для заданного максимально для прямоугольного импульса (при ) и минимально для гауссовского. В частности, уровню соответствуют значения , равные 1,8; 0,94 и 0,48.

Выбор границы спектра по энергетическому критерию в некоторых практических задачах не всегда приемлем. Так, если при обработке импульса требуется сохранить его форму достаточно близкой к прямоугольной, то должно быть гораздо больше единицы. Для иллюстрации этого важного положения на рис. 2.23, б показаны исходный импульс (штриховая линия) и его деформация при усечении спектра на уровнях .

В любом случае при заданной форме сигнала сжатие его во времени с целью, например, повышения точности определения момента его появления неизбежно сопровождается расширением спектра, что заставляет расширять полосу пропускания измерительного устройства.

Аналогично сжатие спектра импульса с целью повышения точности, измерения частоты неизбежно сопровождается растяжением сигнала во времени, что требует удлинения времени наблюдения (измерения). Невозможность одновременно сконцентрировать сигнал в узкой полосе частот и в коротком интервале времени представляет собой одно из проявлений известного в физике принципа неопределенности.

Вопрос о величине произведения длительность X полоса актуален в связи с проблемой электромагнитной совместимости, возникающей при взаимных помехах радиостанций. С этой точки зрения наиболее желательна форма импульсов, близкая к колоколообразной.

2. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА ВНЕ ОСНОВНОЙ ПОЛОСЫ

Для выявления связи между поведением в области относительно высоких частот и структурой сигнала s(t) воспользуемся свойствами таких испытательных сигналов, как единичный импульс и единичный скачок.

Единичный импульс является единственной функцией, имеющей неубывающую спектральную плотность на всей оси частот -

Поэтому можно утверждать, что сигнал , спектр которого вне основной полосы не убывает с ростом , содержит в своем составе дельтафункцию (в реальных условиях достаточно мощный короткий импульс).

Далее, единственной функцией времени, имеющей спектральную плотность вида является единичный скачок и . Следовательно, убывание хвоста спектра сигнала по закону свидетельствует о наличии в функции скачков, т. е. разрывов непрерывности. Но в точках разрыва производная функции обращается в дельта-функцию (с постоянным коэффициентом, равным величине скачка). Поэтому убывание спектра пропорционально указывает на наличие дельта-функции в составе производной Это рассуждение можно продолжить и для производных сигнала более высоких порядков.

Проиллюстрируем сказанное примерами трех сигналов, представленных на рис. 2.24: с разрывом, с изломом и «гладкого» сигнала (без разрывов и изломов).

В первом примере (рис. 2.24, а) производная определяется выражением

и спектральная плотность функции в соответствии с табл. 2.1

Для определения спектральной плотности сигнала , являющегося интегралом от , можно исходить из выражения

В данном случае операция законна, поскольку [см. (2.60)].

При спектральная плотность . Как видно из рис. 2.24, а, это объясняется наличием функции в первой производной сигнала s(t).